Viikon pulma: Olen ottanut graafiset kuvat erään amerikkalaisen oppikirjan sivuilta, ja piirtänyt niiden päälle omia viivoja ja tehnyt sitten opiskelijoille alla olevat tehtävät. Teenkö tekijänoikeusrikkomuksen?
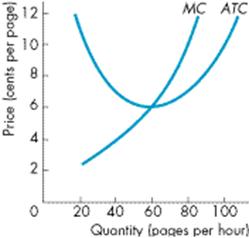
”Kuvaan on piirretty kirjapainon keskimääräisten yksikkökustannusten (ATC) ja rajakustannusten (MC) kuvaajat.
a. Jos yhden sivun painattamisen markkinahinta on 10 senttiä, mikä on ylioppilasien painotalon voiton maksimoiva tuotantomäärä?
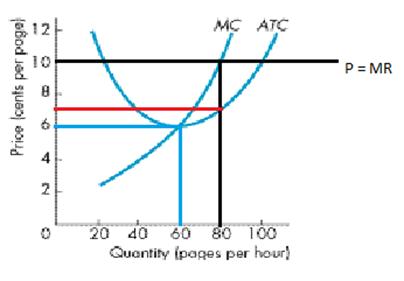
Ensiksi täytyy laskea kirjapainon rajatuotot (MR), mikä on sama kuin markkinahinta täydellisen kilpailun oloissa kaikilla tuotantomäärillä eli P = D = MR, tässä 10 senttiä, katso kuva. Yritys kohtaa siis täysin joustavan kysyntäkäyrän.
Yrityksen voiton maksimointiehto on MR = MC, tässä 80 sivua tunnissa eli pisteessä, missä rajatuotto- ja rajakustannuskäyrät leikkaavat. Sivun myyntihinta on 10 senttiä per sivu.
b. Laske ylioppilaiden kirjapainon voitto. Voitto on hinta miinus kustannukset, tässä 10-7 = 3 senttiä/sivu tai 10*80 sivua – 7*80 sivua = 240 senttiä tunnissa.
c. Onko voiton maksimoiva tuotantomäärä sama kuin kustannukset minimoiva tuotantomäärä? Ei, yrityksen kustannusoptimi on tuotantomäärällä 60 sivua tunnissa, koska tuossa pisteessä keskimääräisten yksikkökustannusten (ATC) kuvaaja on minimissään eli 6 senttiä/sivu.
Mikä on ylioppilaiden painotalon tarjontakäyrä? Se on keskimääräisten yksikkökustannusten ylittävä rajakustannuskäyrä (MC). Joten 6 senttiä/sivu on matalin mahdollinen hinta, jolla yritys voi myydä tuotettaan. Jos hinta olisi alle 6 senttiä/sivu, yritys tuottaisi tappiota. Mitä korkeampi on sivun hinta sitä enemmän kirjapaino tuottaa.”
Toisten teoksia ei saa muunnella ilman lupaa. Tässä tapauksessa kyse ei kuitenkaan ole teoksista. Tehtävissäsi näkyvät kuvat eivät ylitä teoskynnystä, joten niiden kopioiminen oppikirjasta tai verkosta on täysin sallittua. Näitä kopioita saa myös muunnella, liittää osaksi muita oppimateriaaleja ja tuoda julkisuuteen millä tahansa tavalla. Tästä blogista löytyy esimerkkejä huomattavasti monimutkaisemmista piirustuksista, jotka eivät myöskään ylitä teoskynnystä.
Plagiointia kannattaa aina välttää, joten yleensä ottaen kannattaa mainita lähteet, joista on jotain materiaalia ottanut käyttöön. Tässä tapauksessa sekään ei ehkä ole tarpeen, koska alkuperäinen kuva on todella vain yksinkertainen matemaattinen kaavio, jonka voisit itsekin tuottaa muutaman minuutin työllä.